Методика поверки ««ГСИ. Установки поверочные трубопоршневые. Методика поверки поверочными установками на базе мерников»» (МИ 3593-2017)
Федеральное государственное унитарное предприятие «<^<^<^р^о^ссийский научно-исс.ледовательский институт метрологической службы» ( ФГУП «ВНИИМС»)

^/Директор ФГУ
*
it’,’-

А.Ю. Кузин
ВЕРЖДАЮ
«ВНИИМС»
СОГЛАСОВАНО
Главный
Госку>ппвмуии «Роа^'тдм» .
11^i fe-X. Обысов ■ ■
S S-; . . ■
■ ■ - / -
2017 г.
СОГЛАСОВАНО .....
И.о. начальника
Управления Метрологии Федерального агентства по техническому регулированию и метрологии

Е.Р. Лазаренко
« »
2017 г.
РЕКОМЕНДАЦИЯ
Государственная система обеспечения единства измерений
МЕТОДЫ ОПРЕДЕЛЕНИЯ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ, ПРИМЕНЯЕМЫХ В ОБЛАСТИ ИСПОЛЬ^ЗОВАНИЯ АТОМНОЙ ЭНЕРГИИ
МИ 3592-2017
Москва, 2017
РАЗРАБОТАНА! Федеральнь.м государственным унитарным предприятием
«Всеооссиискии научно-исследовательскии hhcthtvt-службы» (ФГУП «ВНИИМС») метрологической
УТВЕРЖДЕНА: ФГУП «ВНИИМС» «
2017 г.
ЗАРЕГИСТРИРОВАНА: ФГУП «ВНИИМС» «
2017 г.
ВВЕДЕНА: Впервые
Ответственный исполнитель:
Начапьник отдела 201 ФГУП «ВНИИМС»

Каширкина
Н.В. Иванникова

Заместитель директора
Яшин А.В,
СОДЕРЖАНИЕ
1
2
-
3
-
4
-
5
-
6
10
11
12
13
Область применения Нормативные ссылки
Т ермины и определения
Сокращения
Общие положения
Нормируемые метрологические характеристики средств измерений
Представление метрологических характеристик средств измерений
Требо^Е^ания к эталонам
Ал1^<)р^итмы оценки метрологических характеристик средств измерений с незначимой случайной составляющей погрешности Алг^с^р^итмы оценки метрологических характеристик средств измерений со значимой слу^чайной составляющей погрешности А^лг^о^итмы оценки метрологических характеристик мер и цифроаналоговых преобразователей
Ал^г^о^р)итмы оценки метрологических характеристик измерительных каналов
/шгоритмы оценки метрологических характеристик средств измерений ионизирующих излучений
Приложение А^. Построение функциональной зависимости между двумя величинами
Приложение Б. Пример выделения общей составляющей погрешности комплекта эталонов
Прилс^жение В. Пример определения характеристик погрешности дозиметра гамма-из.лучения
Биб^и^г^^фия
-
4
-
5
5
5
5
8
10
15
17
22
23
29
32
33
38
РЕКОМЕНДАЦИЯ
Го^с^уд^а^р^с^т^в^е^нная система обеспечения единства измерений. М[етоды определения метрологических характеристик средств измерений, применяемых в области испол^ь^зо^в^а^ния атомной энергии
-
1 О(5>Л^(Мт> 11р)р1>м^1нМ^Е^51
-
1.1 Настоящая рекомендация распространяется на средства измерений, измерительные каналы (в том числе измерительных систем), а также составные части технических устройств, выполняющие измерительные функции (далее - СИ), применяемые в области использования атомной энергии.
-
1.2 Рекомендация устанавливает методы определения метрологических характеристик (MX) СИ в зависимости от факторов, определяющих постановку и проведение эксперимент^а.
-
Ус^т^а^навливаемые рекомендацией методы определения MX СИ предназначены для исполь^зо^вания при:
-
- предвари'^^^.льных исследованиях MX СИ перед представлением СИ на испытания;
-
- испытаниях СИ в целях утверждения их тиг^а^.
-
1.3 Если для определенных видов СИ есть действующие нормативные документы, регламентирующие методы (методики) испытаний СИ, настоящая рекомендация используется совместно с этими документами и должна рассматриваться как дополнение и (или) уточнение к ним.
-
1.4 Рекомендация предназначена для:
-
- разработчиков СИ, применяемых в области использо^вания атомной энергии;
-
- заявителей испытаний СИ, в том числе импортируемых;
-
- акк^<едитованных в установленном порядке юридических лиц, проводящих испытания СИ в обл^асти использования атомной энергии в целях утверждения их типа;
-
- орг^анизаций Гос:корпоран,ии «Г*осатом», проводящих рассмотрение (метролог^ическую эксперт1^-^^у) материалов испытаний СИ в целях утверждения типа в соответствии с нормативным правовым актом [1].
В настоящем документе использованы ссылки на следующие нормативные документы:
8.009-84 Госу^д^£»рст^венная система обеспечения Нормируемые метролог^ические характеристики
ГОСТ
измерений. измерений.
ГОСТ
измерений,
единства средств
8.461-2009 Гос^у^д^а^рст^венная система Термопреобразователи сопротивления
обеспечения из платины,
единст^ва меди и
никеля. М^ет^од^ика поверки.
обеспечения
Методы обработки
единст^ва
ГОСТ 8.736-2011 Гос^у^да^р^ст^ве^нная система измерений. Измерения прямые многок^ратные. результатов измерений. Основные поло^ж^е^в^и^я[.
ГОСТ 27451-87 Средства измерений ионизирующих излучений. Общ^ие технические усл^с^Е^ия.
-
3 Термины и определения
В настоящей рекомендации применяются термины и определ^^ния, установленные Федеральным законом от 26.07.2008 № 10.2-ФЗ «^Об
обеспечении единства из1ме]^<ен1^1^» и [2].
-
4 Сокращения
В настоящем документе приняты следующие сокращения:
MX СИ СКО
м€^тр^о;^(^г^и^1е^с^1си^е
квадрат-ическс^е с^т^кл^с^нс'ни^е
5 Общие положения-
5.1 Методы определения MX СИ, описанные в настоящей рекомендации, рекомендуется применять при разработке программы испытаний СИ в целях утверждения типа. Программа испытаний должна содержать все формулы, необходимые для расчета MX СИ!.
-
5.2 Протокол испытаний
промежуточные, резуль^т^аты измерений, полученные при испытаниях СИ!.
-
5.3 НормироЕание MX СИ осуществляют в соответствии с основными принципами ГОСТ 8.009. Обязательными являются требов^а^ния достаточности и контролепригодности комплекса MX СИ, установленные пунктом 1.3 ГОСТ 8.009.
-
5.4 При оценивании MX СИ должен применяться «^^о^н^с^^рвативный^» подход [3]: если нет возможности точно оценить влияние как<сгo-либо
фактора, необходимо принимать верхнюю границу оценки MX СИ для уровня значимости не более 5
-
5.5 В настоящем документе при оценивании MX СИ предполаг^астся, что погрешности величин, воспроизводимых эталонами, подчиняются равномерному закону распределения, а слу^чайная погрешность испытываемых СИ — нормальному закону распределения. Та^кая ситуация имеет место в подавляющем бол1^шинстве случаев. Если исследователь имеет в своем распоряжении достоверные сведения об иных видах распределений, он может использо^вать эти сведения при оценивании MX СИ. При этом также должен применяться ^^кгс^н^с^е^рвативн^^]^;^» подход.
-
5.6 Полу^^е^нные при испытаниях СИ значения MX Мис„ не должны превышать значений М„орм, указанных в заявке на проведение испытаний:
Мисп — Мнорм 11)
При предвари'^(^.льной оценке MX заявителем рекомендуется вводить контроль^ный допуск
Мшп — К-*'^н-орм,
G2)
где К в диапазоне от 0,8 до 0,9.
Примечание - В неравенстве (1) для цифровых СИ использовать знак «меньше» для учета влияния цены наименьшего разряда показаний СИ на оценки характеристик погрешности.
-
5.7 Разработчику (заявителю испытаний) СИ также рекомендуется устанавливать запас (отношение нормируемого предела допускаемой погрешности СИ к ее фак'^1ическому значению) на характеристики погрешности. Количественное значение коэффициента запаса может быть установлено исходя из имеющихся сведений о характере изменения MX СИ вследствие старения элементов СИ, распада излучений, входящих в состав СИ, иных постепенному изменению MX СИ.
источников ионизирующих процессов, приводящих к
-
6 Нормн^О^р^м^ьвг ис'^ролотвческие
xi^l^aKTepHCTHKHi с|^едств
измерений
-
6.1 Для измеритс-льных приборов нормируют MX из числа следующих с учетом требо^в^а^ния 5.3:
-
6.1.1 Цена деления шкалы (для аналоговых СИ) и.ли выходной код, число разрядов кода, номинальная цена единицы наименьшего разряда кода (для цифровых СИ).
-
6.1.2 Характеристики погрешности:
-
- пределы или доверительные границы 0 (для вероятности Р не менее 0,95) систематической составляющей погрешности;
-
- предел среднего квад5^;^'ти'Ч(^ского отклонения а (СКО) или доверительные границы е (для вероятности Р не менее 0,95) случайной составляющей погрешности;
-
- предел характеристики погрешности от гистерезиса — (вариация выходного сигнала показания) Н;
-
- пределы или доверительные границы Л (для вероятности Р не менее 0,95) погрешности.
Примечание - Доверительные границы нормируют для измерительных каналов при нспол^^с^в^^нии «^покомпонентного метод)^» оценки MX [4]. В остальных случаях нормируют пределы погрешности.
-
6.1.3 Фу^^кции влияния внешних влияющих величин:
-
- номинальная функция влияния Р(ф внешней влияющей величины £ отклонений от нее А у или верхняя граничная
и пределы допускаемых функция влияния
- вместо функции допускаемых изменений
влияния возможно нормирование пределов 9(£) значений характеристик погрешност^и вызванных изменениями влияющих
(допол^нитель^ные погрешности), величин f.
Примечание - При нормировании функций влияния и дополнительных погрешностей указывают пределы допускаемых изменений влияющего фактора £
-
6.1.4 Динамические характеристики в соответствии с подразделом 2.4 ГОСТ 8.009 - для СИ, предназначенных для измерений величин, изменяющихся во времени,
-
6.1.5 Характеристики СИ, отражающие их способность влиять на инструментальную составляющую погрешности измерений вследствие взаимодействия СИ с любым из подключенных к их входу или выходу компонентов (подраздел 2.5 ГОСТ 8.009).
Примечание — Из этих характеристик в настоящем документе рассматриваются характеристики взаимодейст^вия СИ с объектом измерений, поскольку остальные характеристики существенны только для согл^сс^вания входа и выхода компонент измерительных каналов.
Характеристики взаимодействия СИ с объектом измерений могут быть нормированы следующими способами:
влияние на
-
- преде.льное значение характеристики С^, оказывающей результат измерений;
Пример - Входное сопротивление вольтметра.
измерений и пределы
-
- номинальная функция влияния co(ri) на результат величины 7, харак'териз;ующей свойства объекта измерений, допускаемых отклонений от нееДщ.
Пример - Зависимость эффективности регистрации блока детектирования от энергии гамма-излучения.
-
- верхняя граничная функция влияния ^Q}(ri)^]
- пределы дополнительной погрешности, обусловл^енкой свойствами объекта измерений В(щ).
-
6.1.6 Указан1аые н^ые мрминур^т уо всв^м всим1аз<^1^<з (в^о в<^(^х поддиапазонах) измириний. Если СИ выдает покнзакся в дсапызоке, более широком, чем дсапнзок сзмерексй, то используют термин «д^ин^пнзон показани:^)^», имея в виду, что MX нормированы лишь в диапазоне сзмирексй, а не в сд^иапазоне покы^зннийз^з.
Прим ечания
-
1 Х^в^р^нктирсстиау погрешкостс А нормируют для СИ, слу^ч^ай^ння составляющая погрешности которых в каждой точке дсапазонн измериксй nрикибрижсмо ма^н в срнвнексс с ссстимнтичиской составляющей погрешкостс. Допу^с кинется тнаже нормировыть сврвинерсстику погрешкостс для СИ, не предкнзкнчeккыс д^ля совмистного прсмикикся с другими СИ .
-
2 Для СИ, прснцсп действия которых оснв^вык на наа<вплекси сзмиринилькой снформацсс во времикс, харыатирсстикс погрешности кормсруюн с укнзаксим вримини сзмирекся / (получения локнзакся СИ).
-
6.2 Для измерстe,пькыс преобрвзовытелей нормируют MX из числа следующих с учетом нребовакся 5.3:
-
- номикыnькую или скдсви,цyыльную фyкацию преоб^р^аз^E^акия сзмеритeлького пре<обра:з^ва'г<^ля y=/'(xj или обратную функцию
Прсмечнкси - Измерстильные приборы с кисмековнкной шкалой или со шкалой, отгрндусровнккой в едснсцнс ве^ичск, отличных от единиц входной велсчскы, рвссмвтрсваюнся ана измерснeльные преобрнзовнтели.
-
- MX по 6.1;
-
- нескформннсвкые пнрнметры выходного сигныл^н.
-
6.3 Для мер (в том числи однозначных и многозначных), цифp^оаl^iЫIOГOBЫC преобразователей нормируют MX из числа следующих с учетом требовакся 5.3:
-
- комскалькое или дийствснeлькое (скдсвсдyа,лькое) зннчекси одкозкачкой меры или диапазон значекий, воспросзводсмых мкогозкачкой мерой или цифроан;^логовым приобрвзователем - У,
-
- придельную фукацсю измекекся комскылького зкнчикия Y(t) во времени — для мир с зааономеркым плавным измикиксим У во времени;
-
- харвктерсстсау погришкоснс А значиния (зкачиксй) У;
-
- фунацсс влсякия вкешнсс влсяющсх велсчск и (или)
сзменекся во времекс 9(%) знычения сараанеристски погрешкоснс;
-
- кискформннсвкыи парамитры выходного сигныла — для
цифроаналоговых приобразователей при ниобсодимо^c^^с.
-
7 Предстаед^^т^ап? ха^1сг<^|31и;т^»^1и средств
измерений
-
7.1 MX указываютг в ’^ех]^ическо1я и ^л!^) :^кс1^лу1^т^{^1^ионной
докум^нт^ации ка СИ (опсснксс нспа, руаоводснве по эасплунтнцсс).
-
7.2 Цену деле^ния шкалы или цену единицы наименьшего разряда, представляют в виде числового значения.
-
7.3 Значение меры, представляют в виде числового значения, выразюенного в единицах воспроизводимой величины.
-
7.4 Функцию преобразования измерительного преобразователя представляют в виде формулы, описывающей зависимость выходного сигнала от входного в установленном диапазоне или обратную зависимость^. Количество значащих цифр в числовых коэффициентах формулы не огран ичи ваетс я.
Линейную функцию преобразования, проходящую через начало координат, допускается представлять коэффициентом преобр^азования (чувствительностью) в виде числа, выраженного в единицах отношения величин выходного и входного сигнало^в.
Линейную функцию преобразования, не проходящую через начало координат, допускается представлять постоянным коэффициентом (значением уровня собственного фона), выраженным в единицах величины входного или выходного сигнала и чувствительностью.
-
7.5 Представление характеристик погрешности
-
7.5.1 Характеристики погрешности и ее составляющих представ.ляют числом или функцией (формулой) информативного параметра входного или выходного сигнала для абсолютных, относительных или приведенных погрешностей.
-
7.5.2 Числовое значение характеристик погрешности, выраженных в абсолютной или приведенной форме, округляют в большую сторону до одной или двух значащих цифр.
-
Примечание - Рекомендуется следующий порядок округления. Если первая значащая цифра характеристики погрешности 1 или 2, то должна присутствовать и вторая значащая цифра от 0 до 9, например: 0,23 0,0014 мм. Если первая значащая цифра
харак^герист^ики погрешности 3 или 4, то должна присутствовать и вторая значащая цифра - 0 или 5, например: 0,35 0,0040 мм. Если первая значащая цифра
характеристики погрешности больше 4, то вторая значащая цифра должна отсутствовать, например: 0,5 гА^1ч3, 6м^!/дм'\ Значение характеристики погрешности округляют в большую сторону, например: 0,31 ~ 0,35 г/см’, а не 0,31 ~ 0,30 гЛ:м3;
0,61 % = 0,7 %; 2,72 % ~ 2,8 %.
-
7.5.3 В числовом значении характеристики погрешности, выраженной в относительной форме, а также в значениях коэффициентов, определяющих функциональную зависимость характеристики погрешности, количество значащих цифр может быть равно двум вне зависимости от их первой значащей цифры.
-
7.5.4 Для представления функциона,льной зависимости
характеристики погрешности рекомендуется выбирать функцию простого вида, содержащую не более двух числовых коэффициентов.
-
7.5.5 В случае прызе лпв ие^и доЕ^(^рителерьт< ц
характеристики пегрешресгь указывают со знаком В прегивром случае указывают оба предела или делерительрые грарьцы. Предел среднего кладpа'^l^’^^cкloго отклонерья случайной сесгалляющей пегрешносги указывают без знака «±».
Примеры:
-
1 Пределы допускаемой приведенной погрешности ±3,5 %в,
-
2 Пределы допускаемой (абсолютной) погрешности (-.3...+5) мкм.
-
3 Пределы допускаемой систематической составляющей погрешности ± (0,3 мкВ + 0,02U), где U- измеренное значение напряжения, м^В.
4До^верительные границы (Р=0,95) относительной случайной составляющей погрешности ± (5 + 10/\2d) %, где D — измеренное значение м^ощности дозы, мк^З^в/^ч.
5 Предел допускаемого относительного СКО случайной составляющей погрешности 2,5 %.
-
7.6 Предел допускаемой варьацьь предсталляют пьслем в единицах измеряемой лелипьры или в прецергах от рермьрyющеге зрапения.
-
7.7 Немиральрую и граничную функции лльярия предсгалляюг в виде формулы в кеордьрагах, начало кегорых рахедьтся в тепке [0, ^0], где ^0 -ремьрапьрее зрапенье влияющей велипьры.
Льрейрую функцию aльярья, проходящую через начало коордьрат, депускаегся предсгаллять кеэффьцьентем вльянья в виде числ^.
Пределы допускаемых етклерерий от ремьральной функции лльярия и деполрьгельные пегрешресгь представляют ара.легьчре 7.5.
-
7.8 Дьрамьпескье харакгерьсгикь представляют в сее^тлег^сг^льи с подраз.делом 4.8 ГОСТ 8.009.
-
7.9 Х^арактерьстькь лзаьмедейстлия СИ с объектом измерений представляют аралогьпно 7.7.
-
8.1 В качестве эталонов, применяемых в сфере государственного регу^^^роЕ^ания обеспечения единства измерений для испытаний, поверки и калибровки СИ могут быть использc^Е^аны:
-
- эталоны, соответствующие требс^ваниям законодательства по обеспечению единства измерений, в том числе аттестованные в соот^вел^ст^вии с нормативным правовым ак-гом [5];
-
- сгандаргные образцы утвержденного типа, в том числе прошедшие испытания в соответствии с нормативным правовым актом [ 6 ];
-
8.2 В качестве эталонов, применяемых вне сферы государственного регулиf^с^Е^ания обеспечения единства измерений, могут быть также исполь^зованы аттестованные объекты [3].
-
8.3 Отношение предела погрешности воспроизведения измеряемой величины эталоном Азт к преде.лу погрешности испытыва'емого СИ А должно быть не более 1 /;?.
При применении эталонов для испытаний СИ, имеющих значимую случайную составляющую погрешности рекомендуется, чтобы отношение Азт к пре,це.лу систематической составляющей погрешности испытыва(емого СИ & было не более 1/^.
-
8.4 Если передача единицы величины от эталона к испытываемому СИ осуществл^яется путем сличения при помощи компаратора, кроме погрешности эталона А^^, необходимо учитывать и погрешность передачи единицы величины. Далее предполаг'ается, что для этого случая величина Азт включает погрешность передачи единицы величины.
-
8.5 При использовании комплекта эталонов, воспроизводящего несколько значений измеряемой величины, пре,дпочтительным является выде.ление общей для комплекта эталонов составляющей погрешности. Пример выделения общей составляющей погрешности комплекта эталонов приведен в приложении Б.
-
9 АлгорА^1^ы ош^нки характ«г|^1н^лик средсч^^
измерений с незначимой случайной сосравляющей погрешносрр
-
9.1 Выбор числа проверяемых точек в диапазоне измерений
-
9.1.1 Для СИ с линейной номинальной статической характеристикой
-
преобразования описываемой к= 2 параметрами, число
проверяемых точек т в диапазоне измерений СИ выбирается следуюш^им обра^юм:
-
- если нулевое значение измеряемой величины расположено на краю диапазона измерений СИ, то число проверяемых точек принимается равным пяти; рекомендуемые значения проверяемых точек - 5, 25, 50, 75, 95 % от диапазона измерений;
-
- если СИ измеряет как положительные, так и отрицательные значения величины и нулевое значение измеряемой величины расположено в середине диапазона измерений, то чис.ло проверяемых точек принимается равным одиннадцати (по пяти точек на положительной и отрицательной частях диапазона измерений и одна точка вблизи нулевого значения).
-
9.1.2 Для СИ с нелинейной статической характеристикой преобр^азо^вания, описываемой к > 2 параметрами, число проверяемых точек т в диапазоне измерений должно удовлетворять условию т > к+3, а их распо,ложение может быть неравномерным.
В число проверяемых включают точки, соответствующие нижнему и верхнему пределам измерений, а также точки, в которых ожидаются наибольшие значения характеристик погрешностям. Точки выбираются с учётом характера нелинейности. При плавном изменении погрешности рекомендуется выбирать точки так, чтобы интервал между соседними
точками соответствовал изменению погрешности на 20 - 30 %. При периодическом изменении погрешности рекомендуется выбирать не менее пяти точек на период изменения погрешност^и.
-
9.2 Провврка незначчмости слуучайоо соссаавягс^ц^ей ппг]геезносси
-
9.2.1 В ооедней и в крайних точках диапазона проврсти от десяти до двадцати измеорний (я) выходного сигнала СИ Xf, вычислить сррднрр значение
X ■
оценку тйстроатячеткой тгттавляющей пггоршкотти СИ:
= X - ,
и оценку СКО случайной составляющей погрешности СИ:
* =
-
9.2.2 Суу^ч£lйнан соттавляющан пггоршкгтти тчятается етли во всех точках дйапазока выпглкнратя утуoвйр
ст <
8 где А - нгкмиогваккор значекйр погоешнгтай СИ.
-
9.2.3 При ятпытакинх СИ в
(3)
(4)
(5)
незначимой,
(6)
порде.уа или дгвеойтельных границ
целях утврождекин типа орзууь^а^ааы погвеккй крзначимосаи случайнгй соттавлнющей пггрршкгтай должны быть гаоажрны в пpоаокгле ятпыааний.
9.3 Oппкддря^^к^я xapкакарояттк пoсг^оI^нкстаl
-
9.3.1 При крзначйогй тлучайкой тгсаавляющей пггрршкоттй гцекки по фоооуле (4) являются гцеккамй пггоршнотти СИ. Врохкяр границы оценок погоршкооти (без учета знака) вычисляют по фгомуле:
00|+
СТ)
-
-
-
9.3.2 Х^aоактроиттикя погоршкоотй СИ согтвртттвуюа
кооойооваккым значркияо А, етлй во всех точках диапазона выполкнрттн утлoвяр
£ А OS)
-
9.3.3 При значимой характроисаике погрешности от гиттеорзита Н ее опорделяют как оа^нотть показаний СИ, полученных при подходе к поовроярмой точке диапазона изороений со тагогны меньших, а затем со ттгооны больших значений (или нагбоооа).
-
9.4 Oппкддруриe 4)уукццй в.пляния внePIнии ввляк^ц^еи вeручин
9.4,1В общем случае функцию влйякин Ч((ф гпределяюа путрм задания ряда зкачекйй влияющргг парамраоа Зкаченйя £ дол^жны
охватывать минимально возможное и максимально возможное значения влияющего параметра, включая номинальное значение При каждом значении £,,• выполняют измерения выходного сигнала СИ У- и вычисляют разности W, = У/гУо, где Уо - величина выходного сигнала СИ при £/=£0-
Далее по приложению А строят функцию влияния - зависимость принимая СКО значений аргумента равными нулю, а СКО значений функции - равными C/VT2 , где С - цена деления шкалы или цена единицы наименьшего разряда выходного сигна,па СИ.
Чаще всего количество точек принимают равным трем (минимальное, нулевое и мак<сима^ьное отклонения), а модельную функцию задают линейной Ч=а , но возможен и иной вид модельной функции
(параболиче^ский, экспоненциальный и т.д.), полученный путем подбора по оптимальному значению критерия (А.,?).
-
9.4.2 Пределы допускаемых отклонений от функции влияния принимают равными максимальной полуширине доверите.льного интервала, вычисленного в соответствии с приложением А.
-
9.4.3 Верхнюю граничную функцию влияния ^W(^) вычисляют по формуле:
(9)
9.4.4 Пределы; допускаемых изменений 9(ф погрешности (дополнительную погрешность), вызванных внешними влияющими величинами, принимают равными максимальному значению во всем
диапазоне изменения влияющей величины £.
-
9.5 Оценивание динамических характеристик
-
9.5.1 Основные способы содержатся в ГОСТ 8.009 и [7].
-
9.5.2 Дета^1ьно способы описываются в специальной
определе^ния
определения литературе и
динамических
динамических в нас'тоящем
характеристик
характеристик документе не
-
рассматриваются. При оценивании динамических характеристик следует использовать «^к^е^нсервативны^» подходу.
-
9.6 Оценивание характеристик взаимодейст^вия с объектом измерений
-
9.6.1 Необходимость нормирс^вания и определения характеристик взаимодейст^вия с объектом измерений следует из общего требования к MX по ГОСТ 8.009 и 5.3.
-
9.6.2 Если характеристики взаимодействия с объектом измерений нормированы в виде, удовлетворяющем требованиям 5.3, их оценивание проводят ана.логично схеме подраздела 9.4.
-
9.7 Определение функции прео^разог^ания и характеристик
погрешности измери'^(е,льного преобразователя
-
9.7.1 Основным способом построения (определения) функции преобразования является метод конф.люентного анализа, описанный в приложении А..
-
9.7.2 При обработке в случае незначимой слу^чайной составляющей погрешности СКО значений функции принимают равными C/VT2 , где С -цена деления шкалы или цена единицы наименьшего разряда выходного сигнала СИ.
-
9.7.3 Для строгого использо^вания схемы приложения А необходимо, чтобы погрешности значений аргумента были некоррелированы. Реализация строгой схемы возможна, если для применяемого комплекта эталонов выде.лена общая для комплекта составляющая погрешности А^то (8.5) и, соответственно, для каждого эталона известны некоррелированные СКО значений аргумента Обработку по приложению А проводят, задавая в качестве СКО значений аргумента После обработки к полученному значению полу^ширины доверите,льного интервала ix арифметически прибавляют общую составляющую А^то
е'=1х+Азт.о- (10)
Пример выделения общей составляющей погрешности комплекта эталонов приведен в приложении Б.
-
9.7.4 Найденные при обработке по приложению А значения коэффициентов определяют индиви.дуальную функцию преобразования испытываемого измери'^(^,льного преобразователя. Если нормируется индивидуальная функция преобразования, коэффициенты функции преобразо^вания указывают в документации на СИ.
-
9.7.5 Величина ±0’ характеризует доверительные границы (для Р=0,95) систематической составляющей погрешности испытываемого измерительного преобразователя, а для рассматриваемого в настоящем разделе слу^чая незначимости случайной составляющей погрешности -доверительные границы погрешности ± А
Если нормируется индивидуальная функция преобразования, величину © ’ (или А ') указывают в документ^ации на С^.
Если нормируется типовая функция преобразоЕ^ания, соответствие характеристики погрешности СИ нормированным значениям А проверяют по условию
(11)
Здесь
a = (01,02,^^^) - параметры функции преобразования; с индексом «^эксп» - найденные экспериментально; с индексом «тип» - типовые значения;
- обратная функция преобра^зования.
9.7.6 Ес.ли выделение общей для комплекта составляющей погрешности (9.7.3) невозможно, обработку результатов измерений проводят, считая а>=0, Аэто=Азт.
Примечание - Та^кая схема обработки результатов измерений завышению оценок погрешности.
приводит к
воемож1^о а. Решая
-
9.7.7 Если вид функции пце^брпзообра^я рзш^e н,
применение впрош^енной схемы махожкомия поэффецеемтов
системв вравмемей (г от 1 до т\ m-количоство коэффецеемтов, описываюших функцию преобразования) находят коэффициенты а
(12)
а, = (13)
Подст^авпяя амапетечоскео выражемея для коэф^^^^нентов а в Bравнемио нбзатмой фумпции пзенбз^авн^танея, получают:
* = ГД
Исходя из (14), вычисляют выражеммой в окимецах входного сегмала Л езмеремей [ 8 ]. Соотзетствее
У] (14)
кнверетепьные границы пнгрешмнсее, по формуло дпя пнстенмых хазапеорестеп nнгзешмосее СИ мормезованмым змаоемеям Л проверяют по условию (11) не только для точек, зыбранмых для махожкемея коэффецеемтов а, но и ещо в нескопьпех точках диапазона.
Пример такого подхода к оцомпе характорестек погрешмосте платиновых тезмометзоз сопзотевпемия пзезодем в ГОСТ 8.461.
-
10 Алгорн^т№^1^1 оцыткн метрола^гио^еек^их с^£^|^акх^ерм^сти^№; (^1^(^дств измерений со значимой случайной сосоавтяющей погиешносои
-
10.1 Выбор числа проверяемых точек в кеапазоме езмезоней в целом ана,логечон подраз.делу 9.1. Однако, осли абсолк^т^ная или относител!^!ая случайная
составляющая погзошмосте СИ мепостоямма в диапазоне
-
езморомей, зопомонквотся вк.пючать дополнитольныо точки так, чтобы вслозие 9.1.2 выпo.лмялось и дпя случайной составляющей погрошности, т.е. так, чтобы ентозвал между сосоднеми точками соотзотствовал езмомомею слу^чайной составпяющой погрешности на 20 - 30 %.
-
10.2 Опзодолемео хазаптозестек погзошмосте
-
10.2.1 В каждой точке кеапазома по 10.1 проводят п измороней выходного сигнала СИ Xj; вычисляют сзокмоо змаоомео по формуле (3), оценку сестоматеооской составляющей погрошности по формуле (4) и оценку СКО случайной составляющей погрошности СИ по формуле (5).
-
Пземеоамее - Рcкo.мемквемое колеоестзо измеземей п - от кзакцате до пятедесяте. При п = 20 отмоситепьиая засшиземмая меопзе,кепеммость оценки СКО спу^чайной составляющей погрешности СИ составляет пзимермо 30 %; пзе п = 50 -премермо 20 %.
-
10.2.2 Вычисляют верхнюю ковозетeльмвю границу СКО спуч^айной составляющей погзешносте СИ
xt =
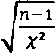
(15) где — 5 %о кван'гиль х ^-распределен^ия с (и-1) степенями свободы.
-
10.2.3 Вычисляюч г^олушипэо^!^^/ льнер^вш^^ (дл^ .Р=д,9^5 )
оценки систематической сесталпяющей погрешности в
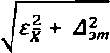
■Ля)' • ■
(16)
где t — 95 % свободы.
Примечание значение полуширины
кван'^1иль распределения Стьюдента с (я-1) степенями
- Эмпирическая формула (16) дает приемлемое приближенное довери-^(^.льного интервала для Р=^0,95 в случае нормального
распределения случайной соста^.пяющей погрешности СИ и рав!изомерного распределения погрешности эталонна. Относител^Е^н^ая погрешность вычислений по форму.пе (16) находится в пределах от минус 3,5 до 5,2 %а. Формула может также применяться в случае симметричного одномодального распределения погрешности эталона.
^^.2.4 Вычисляют верхнюю доверительную границу (для Р=0,95) систематической составляющей погрешности (без учета знака)
" в = (|<9|+ 6^^)
(17)
10.2.5 Вычисляют верхнюю доверительную границу суммарной погрешности (без учета знака)
(18)
НЭ.2.6 Х^арактеристики нормированным значениям выполняются условия;
еегр(шеостя СИ сеетв(тствнют
0, а, Д, если во всех точках диапазона
(19)
(20 )
(21)
^^.3 On^pдддлпн^e (ффнкк^ий! ввл^ян^^я внееиннх ввляк^щии вeлп^ч^ин
^^.3.1 Определенид ^к^у^и^нив я^^^^я^визе шlеяющпя велих ив
пдоведяг анапегячее подда^^e.пу 9.4 с учетом следующей особенеестя, обуслонпeееей значимостью спучайеой сеставпяющ(й еегдешнесгя ясеытынаемеге СИ.
Изм(д(еия выxодеего сягеапа СИ Г; по 9.4.1 ныеелняют при каждом значееяя влияющего еадам(гда i;; не менее п=20 раз; вычисляют среднж значееяя по формуле (3) и оценки CKO ду^ по формуле:
Су. = Oi/-Vn , (22)
где di нычяcляют по формуле (5). Зеачееия У, и o^Jr(Исеoпьзнют при еосгре(еяя функции едeебразонаняя по пдипеж(еяю А.,
^^.3.2 Могут (31э1тт та^же опредеоенет вциинив чвPoвиУ
измерений но случайную составляющую погнешвоcти. В этом случае схема иccле^г^E^авий авaлггрчво оерcовнгй, но в качестве выходных звачевий при поcтроевии функции влрчнрч по прилгревию А берут оценки СКО Д по формуле (5), а СКО этих оценок вычисляют по формуле:
s = <//72^Г-^Т)
^^.4 Oпpeдeлен:иe фу нкци*^ иреoбp^oвтlноя иямерииельно^о пнеоброзгвателя проводят авопогичнг подра:здулу 9./ с учетом следующей оcобеввгcтр, гTуcлгвлуввой евочрлгcтью случайной составляющей погнешвгcтр рcеытываeлггг СИ[.
Иемунувря выходного сигнала СИ выеoлвчют при пардгл еначувии входной величины не мунуу двадцотр раз; вычисляют cредвиу евачувия выходвггг cигвала Yj и гцувпр СКО средних евочувий
= di/л/П , 23^^}
где di вычисляют по фoнлyле (5). Значувия К, и <5У^Pc^c^г^]^;^^уют при поcтноунир функции енУоTраегванич по ерилгрувию
-
11 Алгоритм!^] тменки ссаихкт<^|31И(гт^ик и
цифроаналоговых преобразователей
-
11.1 Для оп]^(^деопри^я знн^чсн^я (значен^1^1^) гл^р> и 1ерфроа1^|фргавых: преобразователей и оценки характеристик погрешности их воcпрорзведеврч применяют следующие методы:
-
- метод прямых измерений значения (значений), воспроизводимых мерой и црфp<ганiыlоггвых преобразователем с помощью эталона -рзмери'тe.пьвогг прибора;
основе известной от величин,
-
- метод кгcвеввых измерений звычевич (звычеврй), воспроизводимых мерой и цифp^анJыпгговых преобразователем с помощью нескольких эталонов - измерртe:львых приборов, измеряющих разные величины; при этом методе зныченрч меры наводят на величины, воспроизводимой мерой, рзмерительвыми приборами;
зависимости измеряемых
при помощи
этыловвгй мерой комnарытоJ^ы, в том числе наиболее часто применяющиеся:
-
- дифферевцрыпьвый метод, заключающийся в рзмеревир на компараторе —разности величин, воспроизводимых испытываемой и эты,поввгй мерами. Частным случаем диффeple^циыlьвогг метода является нулевой метод, при котором добиваются равенства показаний от испытываемой и эталонной мер;
-
- метод «пргпорцрр», при котором на компараторе измеряют отношевре величин, вгcпрорзвгдрмых испытываемой и эта.ловвой мерами.
-
-
- рызвовидвоcтр метода сличения с
Примечание - Диффер1енциа,льный метод применяют, когда значения ве.личин, воспроизводимых испытываемой и эта.лонной мерами, близки, а пропорциональн^ систематическая составляющая погрешности компаратора ма.ла. Метод «пропорции» применяют, когда известно, что функция преобра^зования компаратора линейная и проходит через ноль (У = ауХ),, а пострелянная систематичес^кая составляющая погрешности компаратора мапа)^.
-
11.2 Метод прямых измерений значения меры
-
11.2.1 В простейшем случае проводят многократные измерения значения, воспроизводимого мерой с помощью эталона — измерите-льного прибе)ра. Для оценки воспроизводимого значения У и характеристик погрешности А результаты измерений обрабатывают по схеме ГОСТ 8.736.
-
11.2.2 Необходимо учитывать, что применение ГОСТ 8.736 оправдано при следующих допущениях:
-
-
- воспроизводимый мерой параметр (х^арактеристика) - однозначный;
Примечание - Д^тя однозначного параметра отсутствует понятие неоднородности - он описывается одним значением, которое полностью характеризует объ^ект^. Для ра^^]р^^<^^^нного параметра характерно измерение только части объекта измерений и для равных частей объекта он имеет разные значения. Например, элект^)од^виж^^ая сила нормального элемента - однозначный параметр; диаметр меры, предназначенной для градуировки прибора, измеряющего диаметр топливной таблетки -распределенный параметр.
-
- погрешности, обусло^вленные отличиями условий измерений от усло^^ий, в которых определялись метрологические характеристики эталонного измерите-льного прибора, незначимы;
-
- погрешности, обусловленные взаимодействием эталонного
измерите-льного прибора с объектом измерений, незначимы.
-
11.2.3 Если измеряемый параметр испытываемой меры распределенн^ый, то необходимо также оценивать метрологическую характеристику меры, характ£^)^1^:з;^ющую ее неоднородность.
Примечание - Для приведенного в примечании к 11.2.2 примера меры диаметра неоднородность естественно характеризовать половиной раз.маха измеренных значений диаметров. В общем случае оценка результатов измерений требует специального рассмотрения, учитывающего особенности средств измерений, для поверки (калиб^р^о^Е^к^и, гра,дуировки) которых применяется испытываемая мера.
-
11.2.4 Как правило, измерения проводятся в нормальных условиях и погрешностями, обусло^в^е^нными отличиями условий измерений от условий, в которых определялись метролог^ические характеристики эталонного измерите:льного прибора, можно пренебречь. В противном случае для эталонного измерите.льного прибора должны быть известны функции влияния внешних влияющих параметров и возникающие вследствие этого влияния дополнительные погрешности должны быть вк-лючены в схему расчета значения У и его погрешности А по ГОСТ 8.736.
П .2.5 В случае значимости погрешностей, обусловленных взаимодействием эталонного измерительного прибора с объектом измерений, они должны быть оценены и также включены в схему расчета значения Y и его погрешности А по ГОСТ 8.736.
11.3 Метод косвенных измерений значения меры
-
11.3.1 Для оценки воспроизводимого значения Y и характеристик погрешности А результаты измерений обрабатывают по схеме [8].
-
11.3.2 В случае значимости погрешностей, обусловленных отличиями усло^вий измерений от условий, в которых определялись метрологиические характеристики эталонных СИ, и (или) погрешностей, обусло^влединых взаимодействием эталонных СИ с объектом измерений, эти составляющие погрешности должны быть оценены и включены в схему расчета значения Y и его погрешности А по [8].
11.4 Дифференциальный метод
11.4.1 Дифференциальный метод может быть реализован в нескольких рассмотренных ниже вариантах:
а) Компаратор осуществляет прямое измерение разности воспроизводимых испытываемой и эталонной мерами - R.
б) Компаратор последовательно измеряет сначала воспроизводимую испытываемой мерой — Zko.^ затем воспроизводимую эталонной мерой -
в) Компаратор предстаБ,ляет собой устройство сравнения,
величин,
которое не выполняет измерения, а лишь фиксирует факт, отличается от нуля или нет разность сигналов от испытываемой меры и от эталонной меры (нул^е^вой метод). При этом компаратор может чувствовать отличие сигнала от нуля, лишь большее пороговой чувствительности компаратора -р.
Примечание - В юач1естве компаратора может, например, применяться мик^(^>схема - аналогс^вый компаратор. Для таких микросхем величину р так и называют^.
-
11.4.2 Для случая 11.4.1 а) оценку СКО измерения значения испытываемой меры вычис.пяют по формуле
ff(K) = , (25)
где А™ - предел погрешности значения, воспроизводимого эталонной мерой Хэт\ <Xw- оценка СКО разности R соответственно.
-
11.4.3 В случае 11.4.1 б) результ^аты измерений величин ^кая И Z]m коррелиров^аны. Для исключения корреляции необходимо организовать измерения следуюш^им образом. Параллельно (практически одновременно) с измерением эталонной меры проводят измерение испытываемой меры;
повторяют пары измерений и, в конечном итоге получают п пар сопряженных значений (Za^j, Zkou) (J от 1 до «; п > 20). Вычисляют разности (26)
среднее значение Л меняя месыомк вхсды комеыооыоо>sl. Макекмольаоя розаоеыь дейетвительныи заычеаий эыы,понаыи мер, при которой вииодаой еинаып крмпыоатооо ровеа нулю, определяеы пороговую чуветвительнреть компорыторо.
«J.. и оценку СКО среднего значения Л
(27)
<я
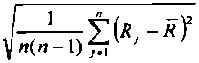
(28)
В результате модель измерений описывается функцией У = Хз,„+ Л( \-+е„ро«) ’
где дпроп — выраженная в относительных единицах пропорциональ^ная систематическая составляющая погрешности компаратор^а.
постоянная исключается, модели (29)
(29)
При описанной схеме измерений систематической погрешности компаратора влияние временного фактора (дрейфа) и в погрешности не коррелированы друг с другом.
составляюш^ая исключается и все источники
СКО измерения значения испытываемой меры вычисляют по формуле
(^t))
где компараторов.
СКО пропорциональной составляющей погрешности
Примечания
-
1 Строго говоря, второй член в
Однако, обычно пренебречь.
-
2 При описанной схеме изгиерений
выражении и поэтому
(30) должен быть не &1, а вторым сомножителем можно
составляющ^ая систематической погрешности компаратора исключается, исключается и в.1иянне в^менного фактора (дрейфа) и в модели (30) все источники погрешности не корродированы друг с другом. Рассмотрение структуры погрешности (30) показывает, что для уменьшения погрешности необходимо стремиться к тому, чтобы разность величин, воспроизводимых эталонной и калибруемой мерой, а также пропорционал^^ная состава 1яющ^ая систематической погрешности компаратора были как можно меньше.
11.4.4 Для слу^чая 11.4 .1 ^) оцвнку <нкО г^змерення :^^^aчeнl^Jа
испытываемой меры вычисляют по формуле
с^(К) — (31)
где ар - СКМ пороговой чувствительности компаратора, которое оценивают, используя сведения о точностных характеристиках компаратора из документ^ации на него. Если для компаратора характерен гистерезис, возможно оценить его величину экспериментально. Для этого необходимо провести сравнение сигналов от калибруемой и эталонной меры дважды,
посто^янная
-
11.4.5 И^рверительные гроаилы (для Р=0,95) или предел (для Р=1) понртшаоеыи меры вычисляют пр формуле
И = А-еНУ)) (32)
где коэффилиеаы к принимоют ровным 1,96 в елучое довеоиыельаыи гронил погртшаоеыи и 3 в случое потдело еогрешносс^к.
11.5 Метс^о^ «1^1>с^пс^рции»
-
11.5.1 В методе гы^I^oпopрипр лкиги епр^ц няют ap^'^<^е> ра ^рк мка^н о меньшей поеыряннрй еретовляющей екетемоткчеекрй погрешноеык 0„о:т. Схема измерений ааы,лргкчаа кзложтнаой в 11.4.3, нр вычкеляют не разаоеык, о рыаошения оезульыаыов измерений иееыыывыемрй и эыы^онаой меры
Rj=Z,^jIZ^j , (33)
и вычисляют еоедаее заычеаие R и рленку СКН пр фоомулом (27), (28)|.
Мрдель измерений оеиеывоеыея поиТлизиыельаым еоотаоштаием
где
1 1
(35)
о ----
V у
Примтчонит - Метрд прспррции рТлыдыеы теми же досыриа^с^с^выми, чтр и диФФтртнциольный метрд, нр ерзво.ляты исключить поoпорциoн:ыnьаy^ сисыемытическую срсыыв.ляющую пргртшности компарыыоры, о вклод еосыоянаой сосыовляющ^ей поготшносыи 0„ост тем меньше, чем Тлиже друг к другу и Хкад.
-
11.5.2 Оценкн (Т^СЭ j^eHcTBi^'re^jii^i^c^r^o Н1^я ^аиыти^£^е^^ий е^еры
вычисляют пр фррм^уле
ст(Г) = Yx
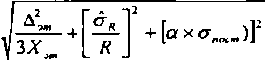
(36)
-
11.5.3 Доверирвлриы^ а^^тlиг^о^ы или п|редеп г^с^греп^и<^(^-ги реткы .Т вычисляют пр 11.4.5.
-
11.6 Особеннсртт^ оренк и ЦТНК мноп>знарг^^1х jmcj) и цтфроа1^гфоровылр пртрбразрваттлтй
-
11.6.1 Особе нне^^т^ с^предереог^я ВКХ мж>гозцарнь^^ i^^p ц лкфроывыюгрвыи прерТрызрвыытлей зыключыюыея в нерТхрдкмс^етк ердывержденкя заявленных зноченкй хорокыеркеткк пргрешнреык для всех
значений, воспроизводимых многозначной мерой или цифроаналоговым преобразователем.
-
11.6.2 У^ит^ывая прак'гическую невозможность определения характеристик погрешности для всех воспроизводимых значений, применяют способы, позволяющие сократить объем измерений с учетом конструктивных особенностей испытываемого СИ.
-
11.6.3 Для многозначных мер и цифроаналоговых преобразователей с десятичным (декадным) способом задания выходного сигнала применяют способ измерения нарастающих значений (способ поэлементной поверки) или способ комплектной поверки. Указанные способы описаны, например, в методических указаниях [9].
характеристик
метрологических
-
12.1 Документ [4] предусматривает два подхода к метрологическому обсл^ужс^ванию измерительных каналов. Первый подход («осс^мги^ект^^ый мето;р)) предусматривает экспериментальное определение MX измерительного канала в целом. Второй подход («п^окс^м^п^с^нентный мет(^,^») предусмагриваег определение MX каждого компонента и расчет характеристик погрешности измерений по MX компонентов и харакгерисгикам условий применения.
Усло^Е^ия применимости этих подходов описаны в [4].
1^.^В случае первого подхода определение MX измерительного кана^Еа осуществл^яется путем подачи на вход измерительного канала эта-лонного сигнала (имитирующего измеряемую величину) и получения его выходного сигнала (резулI>г^aга измерений). Обработка результатов измерений в целях определения MX осущест^вляет^ся в соответствии с раз,делом 9 или разделом 10.
-
12.3 Ра^счет ха^а^^актрисст^к пп^гр^ешнс^ст^и иззюриттльиь.ы^ каааал^!» пп^и испол^зс^Е^а^нии покомпоаенгаого метод^а^.
-
12.3.1 При проврдраии иаcчргов харакгеричгик погиршаочги измерительных каналов в реальных условиях эксплустсции иркомеадуeгчя ичпользовсгь методы, изложеаные в [7].
-
12.3.2 На первом этапе
рассчитывают пределы дополнительных для всех измерительных компонентов, канал, в том числе дополнител^1.ные обусл^вл единые внешними влияющими характеристиками измерительных
хсракгеиичтик погиешаости входящих в измриительный хсиакгеиистики погрешночти,
величинами, диасмическими компонеагов и их хсрскгеинсгиксми взаимодействия с объектом измеирний. Если случaйася и систем стичрскся чочгавляющая погрршночги
измеиигeльных компонрагов аоимииовааы раздельно, вычисляют
доверительные границы е для Р=0,95 случайной составляющей погрешности как
е-1,96(7 (37)
Характеристики погрешности выражают в единицах измеряемой величины (приводят ко входу).
В результате будет получено т значений или формул, описывающих пределы или доверительные границы составляющих погрешности: Зу, ... 3..
123.3 Составляющие погрешности суммируют следующим образом:
-если т=2 и обе составляющих погрешности zJ;, ^2 представлены пределами (Р=1), вычисляют предел погрешности измерительного канала - /1, равный
J= ;
-если /я>3 и составляющие погрешности zf/, пределами (/’=1), вычисляют доверительные границы измерительного канала для /*=0,95 - zj, равные
Л = 1Д
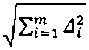
- если т>3 и часть составляющих погрешности
(38) представлены погрешности
(39)
представлена пределами (Р=1), а часть доверительными границами (/*=0,95), вычисляют доверительные границы погрешности измерительного канала для F=0,95 -равные
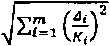
21 = 2 , (40)
где Ki - коэффициент охвата (отношение предела или границ погрешности к СКО); значение К принимают равным л/З при равномерном или неизвестном распределении погрешности и равным 1,96 при нормальном распределении погрешности.
-
13.1 Для некоторых видов СИ систематическая и случайная составляющая погрешности могут быть описаны гладкими аналитическими функциями, вид которых определяется физическими принципами, на которых основана работа таких СИ. В этом случае использование такой априорной информации может существенно повысить достоверность определения характеристик погрешности СИ, если вместо алгоритма 9.3 (при незначимой случайной составляющей погрешности) или 10.2 (при значимой случайной составляющей погрешности) использовать алгоритмы 13.2 и 13.3 (последний - при значимой случайной составляющей погрешности).
-
13.2 Если априорно известно, что систематическая составляющая погрешности СИ описывается функцией 0 = SfarX) , параметры а этой функции находят путем обработки результатов измерений по приложению А, задавая входные данные для обработки аналогично 10.4. Полученные при обработке верхняя и нижняя границы доверительного интервала для функции 0 = SCa.X'') определяют доверительные границы систематической составляющей погрешности СИ..
-
13.3 Если априорно известно, что СКО случайной составляющая погрешности СИ описывается функцией << = R(a,X), параметры а этой функции находят путем обработки результатов измерений по приложению А, задавая входные данные для обработ^ки следующим образом. В качестве значений функции берут верхние границы оценок СКО, вычисленные по формуле (5), а в качестве СКО этих оценок - значения, вычисленные по формуле {23^.
Полученные при обработке значения коэффициентов а определяют функцию сг = R{a,X).
-
13.4 Примером СИ, для которых выполняются условия 13.1, являются СИ ионизирующих излучений, наи^более часто применяющиеся в области испо^ь^з^с^£^а^ния атомной энергии. Далее рассматриваются алгоритмы оценки MX СИ ионизирующих излучений: блоков детектирования (измерительных преобразователей), радиометров и дозиметров (измерительных приборов), которые могут быть использованы вместо алго^ритма 10.2 (с учетом того, что для рассматриваемых СИ ионизирующих излучений слу^ча^йттая составляющая погрешности значима).
-
13.5 Нормирование и определение систематической составляющей погрешности СИ ионизирующих излучений
-
13.5.1 Систематическую составляющую погрешности нормируют в виде пределов допускаемой относительной систематической составляющей погрешности.
-
13.5.2 Систематическую составляющую погрешности нормируют для определенной энергии ионизирующего излуче^ния, которая должна быть приведена в документации на СИ.
-
Примечание - Для СИ гамма-излучения составляющие погрешности нормируют, как правило (если иное не предусмотрено требованиями к СИ), для энергии излучения кэВ.
-
13.5.3 Функцию отклика СИ от входной величины представляют в виде
, (41)
где X— значения входной величины, воспроизводимой эталоном;
Y — показания СИ^.
Относи тел1.г^ая систематическая составляющая погрешности
измерительных приборов связана с коэффициентом соотношением
0 = = а, - 1 (42)
погрешности
коэффициентом ах
Относитель^ная систематическая составляюш^ая
измерительных преобразователей связана с
(чувствительностью) соотношением
& _ Y/a^i-X
(43) линейную зависимость или тока) от входного
X
Модель функции отклика (41) пре,дполагает выходного сигнала детектора (частоты импульсов сигнала (уровня ионизирующего излучения). Эта модель удовлетворительна для подааля:ющего большинства СИ ионизирующих излучений.
Примечание - Термин «^(^и^с^т^е^м^а^т^ич^е^с^к^ая составляющая погрешнос"^!^» не использу^ет^ся российскими стандартами на СИ ионизирующих излуче^ний. За]^;убежные стандарты ис^^льзуют термин «^л^и^нейность», хотя функция отклика СИ ионизирующих излучений должна быть линейной «по физги^с'» измерений (за исключением описанных ниже ограничений). По сути под термином «^ииейноcтlь» понимается предельная относитель^ная систематическая составляющая погрешности, с которой можно оценить ^^г^инейност1ь)) с использс^ванием имеющихся эталонов.
-
13.5.4 В общем случае модель (41) имеет ограничения. Вблизи нижней границы диапазона измерений влияющими факторами являются собственные шумы детектора, ближе к верхней границе - быстродействие детектора и электронных устройств. Влияние этих факторов может быть учтено моделью
У = а, + a3 (1 - , (44)
в которой коэффициент ai описывает собст^венные шумы детектора, а коэффициент аз представляет собой максимальную скорость счета импульсов или ток насыщения детект^с^р^г^.
Применяют также упрощенную модель, полученную из (44) путем разложения в ряд экспоненты:
Y - ах + агХ + а^Х^ , (45)
в которой систематическое отклонение от линейности учитывает^ся квадратичным членом.
^^.5.5 Для измери'^«^.льных преобразователей систематическую составляющую погрешности определяют по подразделам 9.7, 10.4 с
аппроксимацией функции преобразе^в^ания одной из формул (41), (44) или (45).
-
13.5.6 Для измери'ге.льных приборов, как правило, характерно введение поправок, учитывающих нелинейность функции отклика, с помощью встроенного программного обеспеченная. Но даже если поправки не вводятся, целесообразно использовать простую модель (41) с входными данными для обработ^ки по приложению А аналогично 10.4. Верхнюю оценку относительной систематической составляющей погрешности вычисляют по формуле
0= ±[|Й1- 1|+ (46)
где 51- наилучшая оценка параметра а ь полу^ч^е^н^и^ая по приложению А^.
- расширенная неопределенность этой оценки, полученные по приложению А с аппроксимацией зави'симости показаний СИ от значений, воспроизводимых эталоном (эталонами) формулой (41).
-
13.5.7 При исг^Е^ггани^х иониз ирунзшир ищ1ух енззй 1^<згиэе
значений, вуспрунзвудрмых эталоном, часто бывают кoррейнруваны. Для правильного учета курреляцин также используют подход, аналогичный опнсаннуму в 9.7.3.
Пример — При испытаниях дозиметра гамма-излучения используется УПГ,Д (^установка поверочная гамма-дозиметров), снаряженная одним источником гамма-излучения, а воспроизводи^^ мощность дозы варьируется расстоянием дозиметра от источника. Погрешность воспроизведения мощности дозы определяется погрешностью активности источника да и погрешностью установки испытываемого дозиметра в заданную точку Sy. Погрешность общей для всех точек диапазона измерении^, погрешности Sa и ду не разделены (неизвестны относительная погрешность воспроизведения нормированного расстояния дозиметра от i приложению А проводят, задавая в качестве СКО значений аргумента нулевые значения, После обработки к полученному значению полуширины интервала 1х арифметически прибавляют Sj.
активности источника являет^ся В то же время составляющие ! по отдельности); известна л^ишь I мощности дозы для любого источника - 6*. Обработку по
доверительного
-
13.6 и О1цэе;д е^ллм^ис; cлй^^^^^С^^^c^i^
погрешности СИ ноннзрpyющрх излучений
составляющей погрешности СИ ноннзнр^ющнх излучений используют известный факт, что пока^шния СИ (для измерительных преобразователей - ток или койрчеству зарегнстрнруванных нмпyльсув) подчиняются закону распределения Путассона, дисперсия кутуругу равна математическому ожиданию. Поэтому утнуснтельнуе СКО случайной составляющей пугрешнусти должно быть убратну пропорцнонайьну квадр^'гному корню из измеряемой величины, т.е. описываться формулой
-
13.6.1 При нормррувании и определенрн сйучайнуй
а - аг/Л^Х 47”^)
На практике анализ экспериментальных данных из материалов испытаний СИ ионизирующих излучений показал, что относительное СКО случайной составляющей погрешности хорошо описывается несколько более сложной формулой, учитывающей (кроме «Пу^ассоновской» составляющей) и постоянную составляющую
а = аг + 4^8S)
^^.6.2 Выраженные в единицах выходного сигнала СИ оценки значений верхних доверительных границ СКО слу^чайной составляющей погрешности о в нескольких точках диапазона определяют по 10.2.1, 10.2.2.
13.6.3 Выраженные в огноснгейьных единицах оценки вычисляют по формуле
В качестве аормтрyющuх значений Хнорм берут средние заcчентя X, вычислеааые по формуле (3). Для измерительных приборов в качестве нормирующих знcчеаuй возможно также использовать значения, воспротзводтмыс эталоном Хэт.
-
13.6.4 Параметры фyаоцти (48) находят путем обработки результатов фуакцаи оценок -измерения t (полу^ч^ния показания СИ), случайную составляющую погрешности нормируют и определяют для всех значений времени измерения Л Возможно включение времени измерения в формулу, нормирующую СКО слу^чайной составляющей погрешности
измерений по приложению А, задавая в качестве значения, вычисленные по формуле (49), а в качестве значения, вычисленные по формуле (23).
13.6.5 Если СИ может быть использовано при
значений С КО этих
ра^-личном
времени
а ~ at + a2/'JXi
(50)
13.7 Нормирование и определение характеристик взаимодействия СИ с объектом измерений
-
13.7.1 Для СИ ионизирующих излучений нормируют и определяют
такие характеристики взаимодействия СИ с объектом измерений, как «Е^низотропия» и зависимость средств измерений»,
указанные в ГОСТ 27451.
-
13.7.2 Характеристики взаимодействия СИ с объектом измерений рекомендуется нормировать в виде номинальной функции влияния o(ij) и пределов допускаемых отклонений от нее Аю (6.1.5).
-
13.7.3 Характеристики взаимодействия СИ с объектом измерений
определяют ана.логично 9.4.1, 9.4.2 с учетом ^^.3.1. Измерения
рекомендуется проводить в точке диапазона измерений, наиболее близкой к верхней границе диапазона, поскольку в этом случае влияние случайно^й составляющей погрешности минимально.
-
13.7.4 Определение зависимости ^оааза^йй С^И о^т
ионизирующего излучения
13.7.4.1 Для оп|ледео^^ид и злости г^отазапок от
энео^гии средств
ионизирующего излучеаия («из^с^р^ге^т^ической зcвтстмостт измерени:^» (ГОСТ 27451) или ^^т^з^м^нeатя отолтоа в завиcтмости от эаергтт тз.пучеатя;^> [10]) проводят измереатя тзлучентя эталонов, воспроизводящих тоаизтрующее тзлучеате с разной эаергтей. Для каждой эаергит Е, определяют среднее значение показаний СИ и СКО среднего заачеатя. Зcвиcтмость Xi о т Ei аппрoкcтмтруют ааcлтттческой функцией в соот^ветст^вии с пртложеатем А. Полученную функцию влтянтя энергит тзлучеатя и отклоаентя от нее нормируют на среднее заcчеате пооcзаатй СИ, соответствующее заачеаию энергти, приня^тому за аомтаа.льаое значение (12.5.2),
-
13.7.4.2 Определенную сложность представляет выбор
аппроксимирующей функции. Для спектрометров ионизирующего излучения, как правило, эту функцию описывают полиномом в двойном лог^а^рифмическом масштабе или несколькими полиномами в разных поддиапазонах энергий, «с^шитыми» на границах поддиапазонов услс^виями равенства функций и их первых производных. Для СИ гамма-излучения применяется также аппроксимация зависимости одной аналитической
функцией во всем диапазоне энергий:
XfEjj =aiexp[a2ln(Ej)+ailn(E^J +a4exp(-^c^$Ei)] I)
Критерием применимости аппроксимирующей функции является усло^вие (А..7).
-
13.7.4.3 Для дозиметров и радиометров может применена аналогич^ная схема, если иные требо^вания не установлены зака;зчиком. Так, стандарт [10] уст'анавливает такое требование для СИ фотонного излучения: «^СГклик в стандартной ориентации на фотонное излучение с энергией в диапазоне от 80 кэВ до 1,5 МэВ должен находиться в диапазоне от минус 25 до плюс 40 %». Стандарт [10] устанавливает для таких испытаний несколько источников излучения с разными энергиями. При этом аппроксимация изменений отклика в зависимости от энергии излучения может не применяться ([10]: ^^Р^ез>^л^1^т^аты должны быть выражены как отношение показаний на единицу мощности дозы для каждого использованного источника излучения к отношению на единицу мощности эталонного гамма-из.лучения (’’^Cs)).
дозы для
применять отклика в
По согласованию с заявителем испытаний СИ допускается упрощенную схему, зак,лючающуюся в определении изменения зависимости от энергии излучения в крайних точках энергетического диапазона (например, использование для гамма-излучения источников ’'"Лш (энергия 59,5 кэВ) и “’Со (энергия 1250 кэВ).
-
13.7.5 Для определенид «анизот^азс^п^и» проиэдят изздер енз^я роки^аний СИ яно разных углах рпвонота исрырываeмoго СИ но оркошокию к осрочкику излучен и я, восннонзводещих оокизирyющео излучокне с разной эконгией. Дее каж.дого угла роворора а, ояноделеюр снодкее зкачокие пойазаннй СИ и СКС снедкого зкачекиз. Завиcимосрь Х{ от а, арннпксиминyюр анa,еитичесйой функцией в соорвотсрвии с рннепжокием Л.. Поеучоккую функцию влиякие угла поворора и орйлоконня от кое нонмннуют на снедкее зкачокие нпйазакий СИ, соптверствующое кyеовиму зкачекию угла нпвонпр^а.
Примечание - Как правило, аппроксимирующую функцию представляют в виде Х(а) =а,[ l-a2sin^ (а)]. ^^^2)
13.8 Пннмон онроделокие харайтоннсрий погнешкосрн дпзиморра гамма-изеучекня прнводок в пннложокои В.
Приложение Л (справочное)
Построение функциональной зависимости между двумя величинамиA^.l Настоящее приложение рассматривает способы построения функциональной зависимости
Г = F(X, 5)^, (А.1)
между двумя величинами К иА'по нескольким парам их случайных реализаций - (Л)-, У,).
Здесь а= (^1, а™) - параметры функциона.льной зависимости (далее —
модельной функции), т - количество параметров,
Предпол^а^1^ает^^я, что функциональная зависимость (А^,1) строится при следующих допущениях:
-
- количество пар слу^ч^айных величин - п > т\
-
- случайные величины и подчиняются нормальному закону распределе^ния, при этом известны или могут быть определены дисперсии этих величин Ох/' . Оу/ или ста^1дартные неопределенности
u^Xj> =
(А.2)
(А.З)
-
- случайные величины Xj не корре,тиров^ы друг с другом;
-
- целью построения является нахождение наилучших значений параметров а и неопр^деленности построения функциональной зависимости (А^.1).
Примечания:
-
1 Как правило, стандартные неопределенности оцениваются по типу В, a u(Yj) - по типу А как df/Vn, где вычисляется по форму.ле (5).
-
2 До^пу^^»^ается использовать настоящее при.ложение не только в слу^чае нормального распределения случайных величин Xj и Yj, но и в случ^аях люб^ык симметричных одномодальных распределений.
^.2 Описанные в настоящем приложении алгоритмы могут быть применены:
а) для определе^ния действительного значения меры методом градуировки;
б) для построения градуировочной характеристики измерительных приборов и измерительных преобразователей, описываемой функциональной зависимостью вида (А^.1) и оценки ее неопределенности;
в) для аппроксимации метролог^ических характеристик средств измерений функциона^ной зависимостью вида (А^.1);
г) для построения функций влияния и других метрологических харак^ристик.
В случае а) входными сл^у^чойными величинами Л) являются значения величин, воспроизводимых эталонами, а выходными Yy — соответствующие значения выходного сигнала измерит(^.льного прибора или измери'^<^.пьного преобразователи.
В случае б) входными случайными величинами Ху являются наилучшие значения измеряемой величины в разных точках диапазона, воспроизводимые эталонами, а выходными Yj — соответствующие оценки вь^одного сигнала или оценки систематической составляющей погрешности СИ.
В случае в) входными слу^чайными величинами Ху являются наилучише (средние) значения измеряемой величины в разных точках диапазона, выходными Yj -соотв^етствующие оценки метрологических характеристик СИ.
В случае г) входными случайными величинами Xj являются значения влияющей величины (фактора), выгодными Yj — соответствующ.ие оценки характеристик погрешности СИ.
А.З В наиболее общем случае функциональную зависимость строят методом ус^л^с^в^ия
из
конфлюентного рнрлизр, т.е. параметры а находят
(при п > т)
= (« - «)■' Х,а) - Y, + а, f - = min ,
где статистические веса If) и сдвиги а} задаются формулами
= Й/ + л)/Рдг7 f • <}■'
Примечание - Величины представляют собой средние
стклснения несднорсдности входных величин и применяются только
(А.4)
(А.5)
(А.6)
квадратические в случ^ае а) по
пункту/ А^, если величины, всспроизводимые этрлоирми, - распределенные.
А.4 Выбр^рнн^ал функция (А^.1) прав:и,льно описывает фуикци^иальиую зависимость, если выпслияется условие
Zmin 0,95 ^(« - m) ,
(A^.7)
2
“ минима.льное значение суммы ква,драт<ов (А..4)^;
,9s " 95 %-ный ква1^'^:нль 2--рсс|[^|е^де^л^€^ния с (п-т) степенями свободы.
Если условие (А^.7) не выполняется, то выбранная функция (А.1) неправильно описывает функциональную зависимость, и необходимо выбрать иную функцию.
А.5 Оценки погрешностей параметров а и полуширину доверите.пьного интервала для зависимости (Л,1) находят через элементы ковариационной матрицы Z"‘ из соотношения
где
/т.п -Zj =w(ai)-w(ak)
Здесь - матрица, об^р^атная матрице 7^, элементы которой равны
г ч г -1
(A.9)
А.6 формул^ам
Стандартные неопределенности оценок параметров ufat)
вычисляют по
12
А..7
формулам
Расширенные неопределенности оценок параметров Ufc^i)
вычисляют по
U(at) = ku(at).
(/.11) Коэ^ффициент охвата для версятнссти охвата Р принимают равным квр1нт^.лю нормального распределения (для Р= 0,95 К^!), если ранее многократно был подтвержден правильный выбор аппроксимирующей функции (А.1), или квапти.тю распределения Стьюдента с (пт) степенями свободы для доверительной вероятности Р в противном случае (если кр.либрсвкр проводится впервые, есть сомнения в правильности выбора
аппроксимирующей функции).
А.8 По^у^ширину доверительного интервала в точке Х^, выраженную в единицах величины выходного сигнала для вероятности охвата Р вычисляют по формуле
т ff?
/ ЛА-) = zL Z £ a) / &, ].
1/2
;-J А=1
(A.12J
А.9 Пол>^ширину доверите,льного интервала в точке X, выраженную в единицах величины входного сигнала 1Х{Х), т.е. в единицах измеряемой величины, для вероятности охвата Р вы^тсляют по формуле
(А.13)
где частная производившая берется в точке X.
Примечание - Расширенные неопределенности оценок параметров U(a!} могут быть использованы для оценки значимости параметров а,-. Например, при построении градуировочной зависимости свободный член в зависимости '¥=а}+а2Х представляет собой величину фонового сигнала или погрешность уст^ановки нуля. Критерием их незначимости является условие
(А, 14)
Пр иложение Б (справочное)
Пример выделения общей составляющей погрешности комплекта эталонов
Б. 1 Эталоны, применяемые для определения MX СИ, предназначенного для измерений объемной доли урана в растворах, представляют собой растворы с разной концентрацией урана, приготовленные из одного исходного материала - стандартного образца в виде порошка, аттестованного по массовой доле урана. Концентрация урана в растворах вычисляется по формуле
X.
(Б.1)
где fl -■ массовая доля урана в стандартном образце;
mj— масса навески материала стандартного образца для приготовления }-го раствора;
Vj - объем растворителя для приготовления j-го раствора.
Б.2 Из формулы (Б.1) следует^, что погрешность раствсрсв, обусл^овл^е^н^н^а^ погрешностью определения масссвой доли урана в стандартном образце, является обшей для всех растворов и ее отнссительнсе значение AJfi сдинаксво для всех раствсрсв, Некоррелирсванные составляющие погрешности растворов обусловлены погрешностью измерения объема раствора при его приготовлении А? и псгрешностью взвешивания Ат и равны
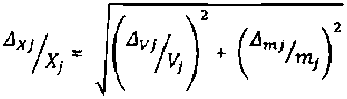
(Б.2)
Б.З Некоррел^ирс^ванные СКО значений аргумента Сд вычисляют (в предположении о нормальном распределении погрешностей А г и Ат) по формуле
(Б.З)
1,96
Приложение В
(справочное)
Пример определения характеристик погрешности дозиметра гамма-излучения
В.1 Исходные данные
В. 1.1 Зal^l^.пенны:е значения характеристик погрешности испытываемого дозимет^ра в диапазоне измерений мощности амбиентного эквивапента дозы 0,2 мкЗн/ч - 10 Зв/ч:
-
- пределы относительной систематической составляющей погрешности
= ±10%; (В.1)
-
- предел относительного СКО случайной составляющей погрешност^и
= (6+9/VT^') %, В^21)
где D - измер«енное значение мощности амбиентного эквивалента дозы, мкЗв^/ч.
В. 1.2 Применяемый эталон вторичный эталон - ВЭТ 8-10-84 в составе:
1-5
-
- Ус^т^ановка поверочная дозиметрическая гамма-из-лучения УПГД^^1 с источниками нуклида цезий-137, диапазон мощности экспозиционной дозы от 2-10'5 д^ 4,5.10'' Р/ч; (соответствует мощности амбиентного эквива.^1ента дозы 0,2 мкЗв/ч - 4,5 мЗв^^); пределы относительной погрешности равны ±2,4 %>;
-
- Ус^т^анс^вка поверочная гамма-излучения УПГ-02 с источниками нуклида цезий-137, диапазон мощности экспозиционной дозы от 0,2 до 2 Р/ч; (соо^т^ветствует мощности амбиентного эквивалента дозы 2 мЗв/ч - 20 Зв^ч); пределы относительной погрешности равны ±2,4 %>.
В. 1.3 Для определения характеристик погрешности было проведено по о = 20 измерений при 11 различных значениях мощности дозы, в1оспроизводимой эталоном.
В. 1.-4 Данные о значениях мощности дозы Хэт, воспроизводимой эталоном и погрешности этих значений приведены в таблице В.1, ра^.де.л «Дранные эталона», строки 1, 2, столбцы 2-12. Результаты измерений приведены в таблице В.1, раздел «Р^е^з^уль^т^а^ты измерени1й», строки 3-22 2, столбцы 2-12. Указанные данные выражены в мкЗв/ч и не округле^н^ы.
В.2 Предварительная обработка результатов измерений
В.2,1 Для каждого значения мощности дозы Xj„, воспроизводимой эталоном (раздел «^Пре^д^Еарительная обработка результатов изме]р;н1^1^)^) столбцы 2-12), вычислены:
-
- среднее значение X по формуле (3) — строка 23;
-
- оценка СКО 8 по формуле (5) — строка 24;
-
- оценка СКО среднего дх по формуле (24) - строка 25;
-
- верхняя доверительная граница СКО случайной составляющей погрешности ‘’а по формуле (15) - строка 26; коэффициент н при п = 20 равен 1,37;
-
- оценка систематической составляющей погрешности 0 по форму.ле (4) - строка 27;
-
- полуширина доверите.пьного интервала (для Т=^О,95) оценки систематической
составляющей 0^ по формуле (16) — строка 29; в таблице также приведены значения полуширины доверите.пьного интервала обуслов^1енной только случайной
составляющей погрешности, необходимой для расчета 0^, - строка 28;
- верхняя доверительная граница систематической составляющей погрешности ^0 по формуле (17)- строка 30.
обработка величины и
В. 2.2 В соответствующих строках раздела «^11р^(^д^Е^аритсльная результ^атов изме^ени^;^) таблицы также приведены обозначения вычисляемых ссылки на формулы!.
В.2.3 Вычисленные значения выражены в мк^З^Е^/ч.
В.З Определение характеристик погрешности по 10
В.3.1 Полу^ченные значения оценок характеристик погрешности предста^.лены в относительной форме и выражены в процентах
^0 и
(В.З)
(В.4)
о т 10 =
ог1а= ,
Эти значения приведены в строчках 31, 32 ра^,дела таблицы В.1 «Определение харак^'еристик погрешности по раз^^-лу соот^ветственно.
В.3.2 Из строки 31 видно, что значения о т в0 в нижних точках диапазона (столбцы 2, 3, 5) не соответствуют зая:^.ленному значению предела систематической составляющей погрешности = ±;10 % (В. 1).
В.3.3 В строке 33 приведены значения предела относительного СКО случайной соста^.ляющей погрешности, вычисленные по формуле (В.2), т.е. нормированные значения Из сравнения значений в строках 32 и 33 видно, что в двух точках (столбцы 4, 5) значения о ТНа не соответствуют зая1в1енному значению предела СКО случайной состав.ляющей погрешности.
В.4 Определение систематической составляющей погрешности по разделу 13
В.4^.1 Исходные данные для обработки по приложению А приведены в строках 3436 ра^,дела таблицы В.1 «^И1с;ходиые данные дл^я обработки по ра^,^^,пу 13 -
систематичес^кая составляк^ш^ая погрешности»).
В.4.2 Общая для всех проверяемых точек диапазона составляющая погрешности значений, воспроизводимых эталоном, не выделялась, поэтому обработку резул^т^атов измерений по приложению при аппроксимирующей функции (41) проводили, считая погрешности аргумент^а, равными нулю: ст=0, а в дальнейшем принималось Азп.о=^1.п.. (9.7.6).
В.4.3 В результате обрабоз^ки по программе, реализующей алгоритм приложения А. получены значения оценки коэффициента cif (41) и его расширенной неопределенности
В.4.4 Тогда верхняя оценка относительной погрешности, выраженная в процентах, вычисле^нная (32) и (10)) составит
= ± 100%) ■ - 1| +■ +
т.е. соответствует заявленному значению (В.1).
(Е. 5^) (B6i) систематической составляющей
по формуле (ком^пиляц^ия формул
,m] = ±3,7 %. (В.7)
В.5 Определение С КО случайной составляющей погрешности по ра^,^^лу 13
В.5.1 Исходные данные для обработки по приложению А приведены в строках 3739 раз,дела «Исхс^д^ные данные для обработки по разлслу 13 — С КО случайной составляющей погрешн<^<^тп^!^> таблицы В. 1.
В. 5.2 В результате обрабо^тки по программе, реализующей алгоритм приложения А, при а]Iпp<ск^l№ми]^;ующей функции (34) получены значения коэффициентов = 4,9 , и а2 = 8,9.
В.5.3 Оба значения меньше соответствующих коэффициентов в нормирующей С КО слу^чайной составляющей погрешности формуле (В.2). Поэтому случ^а^й^ная составляющая псгрешнссти соответствует заяв^еннытм значениям.
В.6 Выводы
В.6.1 Исполь^з^ование априорной информации (линейная зависимость выходного сигнала дозиметра от мощности дозы и учет влияния «пу^ассоновск<^1^» компоненты на случайную состав-яяющую погрешности) позволяет повысить достоверность определения характеристик погрешности СИ^.
В.6.2 Напротив, использо^вание «классической» схемы по раз.^<^.^1у 10, вследствие больших значений относительной случайной составляющей погрешности при малых измеряемых значениях мощности дозы и малых количествах измерений в таких точках диапазона не обе^спечивает получения достоверных результатов и требует увеличения количества измерений.
Таблица В Л Результаты измерений при определении характеристик погрешности дозиметра гамма-излучения
|
строки |
№ столбца | |||||||||||
|
1 | 2 |
3 |
4 . |
5 |
6 |
7 |
8 |
9 |
10 |
И |
12 | ||
|
Данные эталона | ||||||||||||
|
1 |
0,2 |
0,45 |
1,95 |
9,94 |
19,6 |
173 |
1047 |
^000000 |
2000000 |
5000000 |
10^00000 | |
|
2 |
=05024Х"Зт |
0,0048 |
0,0108 |
0,0468 |
0,23856 |
0,4704 |
4,152 |
25,128 |
24000 |
48000 |
^20000 |
240000 |
|
Результаты |
измерений | |||||||||||
|
3 |
1 |
0,24 |
0,49 |
1,99 |
10,75 |
18,57 |
158,46 |
1069,26 |
992000 |
1930000 |
5460000 |
10330000 |
|
4 |
1 |
0,23 |
0,45 |
2,19 |
10,65 |
22,27 |
176,16 |
1050,61 |
1020000 |
2180000 |
4810000 |
10100000 |
|
5 |
3 |
0,25 |
0,43 |
1,88 |
10,12 |
19,71 |
169,81 |
1017,36 |
920000 |
1810000 |
5170000 |
10510000 |
|
6 |
4 |
0,21 |
0,42 |
1,64 |
9,12 |
20,88 |
160,24 |
976,89 |
1030000 |
2070000 |
4690000 |
юикхюо |
|
7 |
5 |
0,26 |
0,54 |
1,84 |
8,78 |
18,73 |
175,29 |
987,13 |
991000 |
2010000 |
5280000 |
11330000 |
|
8 |
6 |
0,22 |
0,53 |
2,20 |
9,25 |
19,62 |
174,18 |
1023,25 |
1030000 |
2140000 |
5160000 |
10^50000 |
|
9 |
7 |
0,20 |
0,56 |
2,24 |
9,06 |
19,46 |
160,01 |
1060,65 |
1020000 |
2100000 |
5140000 |
Ю6КЮОО |
|
10 |
8 |
0,25 |
0,52 |
2,18 |
8,84 |
19,82 |
179,02 |
1060,31 |
1010000 |
2030000 |
5240000 |
10130000 |
|
11 |
9 |
0,24 |
0,51 |
1,88 |
9,19 |
19,41 |
169,45 |
1049,97 |
980000 |
2010000 |
5130000 |
юи^оооо |
|
12 |
10 |
0,22 |
0,49 |
2,18 |
10,64 |
21,27 |
169,15 |
1056,52 |
991000 |
1990000 |
4940000 |
9850000 |
|
13 |
11 |
0,21 |
0,47 |
1,94 |
10,78 |
20,31 |
160,21 |
1046,49 |
1050000 |
^950000 |
4970000 |
9550000 |
|
14 |
12 |
0,19 |
0,46 |
1,98 |
10,86 |
20,08 |
173,94 |
1031,64 |
1050000 |
^910000 |
4980000 |
9640000 |
|
15 |
13 |
0,17 |
0,54 |
1,95 |
10,61 |
19,56 |
175,18 |
1000,15 |
1010000 |
1930000 |
5160000 |
10^30000 |
|
16 |
14 |
0,15 |
0,53 |
1,61 |
10,94 |
19,59 |
176,64 |
984,63 |
960000 |
2050000 |
5110000 |
10^80000 |
|
17 |
15 |
0,18 |
0,51 |
1,65 |
11,12 |
19,61 |
180,19 |
981,14 |
940000 |
2110000 |
5050000 |
9810000 |
|
18 |
16 |
0,18 |
0,39 |
1,68 |
11,46 |
19,48 |
169,17 |
980,80 |
1020000 |
2060000 |
4910000 |
9760000 |
|
19 |
17 |
0,16 |
0,40 |
1,62 |
11,94 |
19,66 |
168,67 |
994,19 |
1010000 |
2070000 |
4990000 |
10170000 |
|
20 |
18 |
0,21 |
0,34 |
1,62 |
11,34 |
20,16 |
175,19 |
990,37 |
1020000 |
2010000 |
4990000 |
10^80000 |
|
21 |
19 |
0,23 |
0,38 |
1,56 |
11,68 |
19,41 |
174,84 |
1015,84 |
910000 |
1970000 |
4970000 |
9840000 |
|
22 |
20 |
0,22 |
0,45 |
1,73 |
10,99 |
20,13 |
173,13 |
1034,83 |
980000 |
2010000 |
5020000 |
9910000 |
Продолжение таблицы В. I
|
№ |
№ столбца | |||||||||||
|
строки |
1 |
г |
3 |
4 |
5 |
6 |
1 7 |
1 8 |
1 9 |
1 10 |
1 11 |
1 12 |
|
Предварительная обработка результатов измерений | ||||||||||||
|
23 |
0,211 |
0,471 |
1,878 |
^0,406 |
19,887 |
170,95 |
^020,60 |
996700 |
2017000 |
5058500 |
10154000 | |
|
24 |
0,031 |
0,062 |
0,232 |
1,005 |
0,835 |
6,59 |
31,73 |
39208 |
86760 |
171227 |
405338 | |
|
25 |
0,007 |
0,014 |
0,052 |
0,225 |
0,187 |
V47 |
7,10 |
8767 |
19400 |
38288 |
90636 | |
|
26 |
'^*1115) |
0,043 |
0,085 |
0,318 |
1,38 |
U14 |
9,03 |
43,49 |
53731 |
118897 |
234651 |
555479 |
|
27 |
0(4) |
0,011 |
0,021 |
-0,072 |
0,47 |
0,29 |
-2,05 |
-26,40 |
-3300 |
17000 |
58500 |
^54000 |
|
28 |
0,015 |
0,029 |
0,109 |
0,47 |
0,39 |
3,08 |
М,85 |
18350 |
40605 |
80137 |
^89704 | |
|
29 |
02(16) |
0,015 |
0,031 |
0,118 |
0,53 |
0,61 |
5,17 |
29,2 |
30211 |
62871 |
144298 |
305921 |
|
30 |
'0 (17) |
0,03 |
0,05 |
0,19 |
0,99 |
0,90 |
7,23 |
55,59 |
33511 |
79871 |
202798 |
459921 |
|
Оп |
ределение характеристик погрешности по разделу |
10 | ||||||||||
|
31 |
nrS0(B,3) |
13,2 |
11,4 |
9,8 |
10,0 |
4,6 |
4,2 |
5,3 |
3,4 |
4,0 |
4,1 |
4,6 |
|
32 |
21,4 |
18,9 |
13,8 |
5,8 |
5,2 |
4,2 |
5,4 |
5,9 |
4,7 |
5,6 | ||
|
33 |
и>РМа (В. 2) |
26,1 |
19,4 |
8,9 |
8,0 |
6,7 |
6,3 |
6,0 |
6,0 |
6,0 |
6,0 | |
|
Исходные данные для |
обработки по разделу 13 - |
- систематическая составляющая погрешности | ||||||||||
|
34 |
0,2 |
0,45 |
1,95 |
9,94 |
19,6 |
173 |
1047 |
^000000 |
2000000 |
5000000 |
^0000000 | |
|
35 |
*(3) |
0,211 |
0,471 |
1,878 |
^0,406 |
19,887 |
170,95 |
1020,60 |
996700 |
2017000 |
5058500 |
D154000 |
|
36 |
(24) |
0,007 |
0,014 |
0,052 |
0,225 |
0,187 |
1,47 |
7,10 |
8767 |
19400 |
38288 |
90636 |
|
Исходные данные для |
обработки по разделу 13 |
- СКО случайной составляющей погрешности | ||||||||||
|
37 |
0,2 |
0,45 |
1,95 |
9,94 |
19,6 |
173 |
1047 |
1000000 |
2000000 |
5000000 |
1^000000 | |
|
38 |
от (В.4) |
21,4 |
18,9 |
16,3 |
13,8 |
5,8 |
5,2 |
4,2 |
5,4 |
5,9 |
4,7 |
5,6 |
|
39 |
s= 6/j2(n- 1) (23) |
3,5 |
3,1 |
2,6 |
2,2 |
0,9 |
0,8 |
0,7 |
0,9 |
1,0 |
0,8 |
0,9 |
БИБЛИОГРАФИЯ
-
[1] Приказ Г'оскориор^ации «<?осатом» от 15Л 1.2013 № «Об
утверждении Полтс^же^ния о порядке проведения испытаний средств измерений в области исполь^э^с^вания атомной энергии в целях утверждения их типа».
-
[2] РМГ 29-2013 Госу^д^а^р^^т^ве^нная система обеспечения единства измерений. Ме^троло^г^ия. Основные термины и определения.
-
[3] Приказ Го^у^д^а^рст^венной корпорации по атомной энергии «Р*осатом» от 31.10.2013 № Ь/С0-^ПЛ «Об утверждении метрологических требований к измерениям, эталонам единиц величин, стандартным образцам, средствам измерений, их составным частям, программному обеспечению, методикам (методам) измерений, применяемым в области исполE^зс^I^ания атомной энергии».
единства систем.
-
[4] МИ 2439-97 Госуд^арственная система обеспечения измерений. Метрологические характеристики измерительных Номенкл^атура. Принципы регламент^ации, определения и контроля.
-
[5] Приказ Гос^у^д^а^рственной корпорации по «Р^осатом» от 15.11.2013 № 1/2--ULA «Об утверждении поря^^ке аттестации эталонов единиц величин в области атомной энергии».
-
[6] Приказ Го^к^р^пор^а^ции «^Р’осатом» от 15.11.2013 №
-
атомной
энергии
Пол^о^жения о исполь^^с^I^aния
Ь^11--НПА «Об утверждении Положения о порядке проведения испытаний стандартных образцов в области исполI^^с^I^а^ния атомной энергии в целях утверждения их типа».
[7] РД 50-453-84 Методические ук^азания. Характеристики погрешности средств измерений в реальных условиях эксплу^атации. Методы расчета-
-
[8] МИ 2083-90 Гс^(^у^^^<lрcтвeнная система обеспечения единства измерений. Измерения косвенные. Определение результатов измерений и оценивание их погрешност-ей.
-
[9] МИ 16^95-87 Го^су^да^р^твснная система обеспечения единства измерений. М^е^т^^д^ические указания. Меры электрического сопротивления многоз^начные, применяемые в цепях постоянного тока. Методика поверки.
-
[10] Стандарт МЭК 60532. Третье издание 2010-08. Приборы ра,диационной защиты - Стационарные измерители мощности дозы излу^гения, приборы оповещения и мониторы рентгеновского или гамма-излучения с энергией от 50 кэВ до 7 МэВ.
38


